The 37% rule
Introduction
It’s now week 5, and you’re still squatting on the floor of that smug bastard who started looking for houses during the last exam period.
Dreams of a two storey O’Connor townhouse opposite The Ruc are long gone, your aspirations have slipped past Lyneham, past Mitchell to faded white towers of Belco. In your darkest moments – on that blow-up mattress you call a bed – you’ve occasionally considered Tuggeranong.
You’ve been given a further month reprieve, on top of the two months that were only meant to be two weeks. And then it’s the house or the streets.
You went to the best private school in Sydney, got an HD once, you study Law! Things were never meant to be like this.
Perhaps, with a toastie machine and some baby wipes a pod at Chiefley could be cosy once it drys out?
Could you fly in from Sydney and fill your timetable up on Tuesday and Wednesday? Not like you were going to go to uni any other day after the first week.
Book a hostel for a week, fall madly in love with an SR, marry them, then live in their double room?
Assumptions
The best news about these five weeks of turmoil is you now have your pick of the houses. Your fanciful plans are humorous memories.
All N you apply for, want you, and you’re five nineteen-year-old mates. Those landlords left it too late, and now they will suffer noise complaints and stained wine carpets.
So, you’ve got a month to pick the best house, how should you do it?
With the only caveat being, once you see a house, you must take it or lose it.
Pick too soon, and you won’t have seen the best house. Too late, and you’ll be left with regrets and a faint smell of cat urine.
We’ll also assume this dream house has an equal likelihood of popping up anywhere in your list of potential houses.
Strategy
Go to M out of the N inspections, then settle for the next house that is better than the previous (M/N) % .
The house you are aiming for is called X, so we need to find (M/N)% to maximise our likelihood of finding it.
Maths behind it all
line them up
Let’s calculate the probability P(M,N) of picking X if you date M people out of N and then go for the next person who is better than the previous ones.
The overall probability is naturally a sum of several terms:

If the first house is the best, tough luck, you’ll miss it, and the first M houses. So the likelihood of them is 0.
But if the newly refurbished Turner 6-share, with a pool for only $ 500 a week is the (M+1)th you’re in luck.
As it must be better than all previous house:
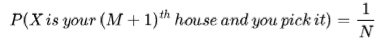
The greater the N, the smaller this chance, so let’s consider the (M+2)th house. This means the (M+1)th didn’t have a higher rating than the previous M, and the probability of the (M+2)th being the best is (1/N) again:
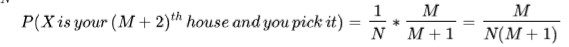
Now, for the (M+3)th, we repeat the argument for the (M+2) th case, and get:
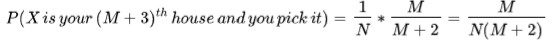
That there are finitely many houses in Canberra is quite a reasonable assumption to make, as there is only a population of 381,000. So we can keep enumerating out the argument until we get to the point where all but the final ( (N−1)th cases) , as for the final one. It doesn’t matter. You got the house with the neighbours who are learning how to yodel on one side and cook meth on the other.
This final case will be:
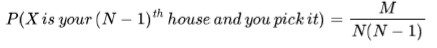
When we collate all this, we get:
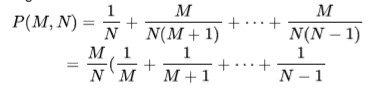
pick your target
So the condition we want to place on P(M,N) is: P(M-1, N) < P(M,N) and P(M+1,N)< p(M,N).You set up the conditions we specify, do some algebra and find a rule. Firstly that: P(M-1, N) < P(M,N) goes to:
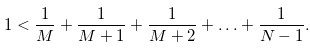
And next, that P(M+1,N)< p(M,N) goes to:
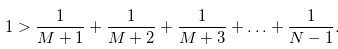
We now need to find the M that satisfies both of these conditions.
example
So, you’ve filled in so many applications that you are now sick of your name and nonchalant about the lie regarding your financial stability.
And grad job applications and assignments have got on top of you so you could only apply for five houses, so we get the following:
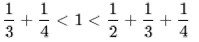
We would get M =2, so the first 2 houses should be ignored. Then you accept the next best one.
knock ’em down
So we have our equation now:
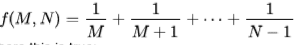
And our problem is to find M where this is true:
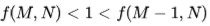
It is clear we are building squares above and below the line (1/x) Firstly above (the highest point on the curve is where the top of the square is):
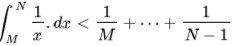
And below (lowest point on the curve is where the top of the square is):
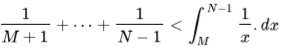
With these equations we are making rectangles 1 unit apart, then multiplying them by their position on the line 1/x, so if we were looking at the rectangle(likelihood of choosing the right one is increased by having this here) at the house being between M+5 and M+6, we make our rectangle by multiplying the width: (M+6) –(M+5) =1. By the height of the line at the point we will depend on whether we do the top or bottom value, it will be: 1/(M+5) and 1/(M+6) respectively. Multiplies by one, they stay the same.
Now if we integrate (this adds up all our increases in additional chances) our term to solve it, this sums up:
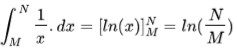
While our other term goes to:
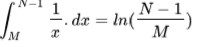
And as (N/M)≈(N−1)/M when N and M are large (just put some fake numbers in and try!). We can just work on the term for our lower bound, then we get:
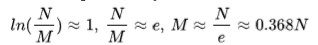
So the best place to execute our plan, to select the next best house(the house before is M) after all the ones we have seen is at around 0.37 multiplied by the total number of houses – this is just 37%.
Veranda and a picketfence
You’ve done the maths, your housemates thought you were too weird and left you and so you took to craigslist to find new housemates. But that doesn’t matter, by picking the next house better than all the first 37% you saw, you found your dream house.
Dave who is coming down from Perth for an undisclosed line of work might think shitting in the garden is fine as “it’s all dirt anyway”.
Jimmy might ruin your date night every week by bringing around a different group of friends and all taking dark web hallucinogens.
And Andy will be arriving tomorrow with his bond, backpay of rent and all the lounge room furniture until the end of the contract.
But at least you have your castle, and it was all because of the 37% rule.
We acknowledge the Ngunnawal and Ngambri people, who are the Traditional Custodians of the land on which Woroni, Woroni Radio and Woroni TV are created, edited, published, printed and distributed. We pay our respects to Elders past and present. We acknowledge that the name Woroni was taken from the Wadi Wadi Nation without permission, and we are striving to do better for future reconciliation.
