This is, I admit, a sensationalised title. No, Tony Hawk has not challenged Hannah Fry to a fight. But some mathematicians have proven something that may seem shocking to the skateboarding world.
Some background: in skateboarding, a flip trick is where you jump in the air and flip your board in some way before you land. There are basics like the Ollie (stomping on the back of the board to launch it in the air) and the shove-it (jumping while the board does a 180° in the air under you). More interesting tricks include the kickflip and the varial kickflip. Look at the Wikipedia page and you can see how varied they are.
Recently, four mathematicians authored a paper, ‘Skateboard Tricks and Topological Flips’, proving that there can only be four flip tricks.
Does that mean skateboarders have been rehashing the same four tricks all this time? No, but it’s a long answer.
Totally Orthogonal Tricks
In ‘Topological Flips’, a skateboard is modelled as an orthogonal frame.
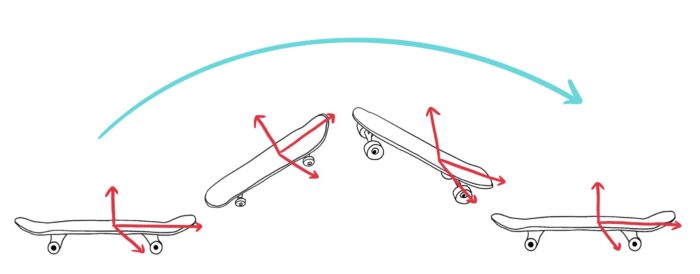
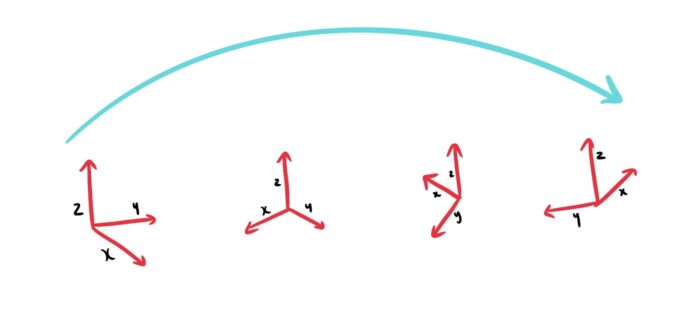
Abstractly, we can represent a skateboard by three vectors (arrows). The y-vector – points towards the front of the board. The z-vector points out from the top. The x-vector points to the right of the board.
The frame is all you need to visualise a flip trick. For example, an Ollie could be drawn like this:
Figure 1: A representation of an Ollie.
In principle, you could identify the trick entirely by seeing how the frame moves. For example, if you erase the skateboard, a shove-it looks like this:
Figure 2: A representation of a shove-it.
Notice how the x and y-vectors rotate while the z-vector stays put – imagine the skateboard spinning!
In most flip tricks, the skater starts on flat ground, executes the trick, and lands with their board facing forwards or turned around 180°.
Say the ‘flat on the ground, facing forwards’ frame is I, and the ‘flat on the ground, facing backwards’ frame is O. Then a flip trick would be defined as a continuous progression of orthogonal frames, starting at I and ending at I or O.
Mathematicians would call this a continuous path (or continuous curve). But it’s not a path through physical space. The space in question is the space of 3D oriented orthogonal frames, called SO(3) by mathematicians.
This is a 3-dimensional space. That’s a total coincidence – SO(4), for example, is 6-dimensional. And SO(3) is curved in hard-to-imagine ways and doesn’t look quite like the 3D space we live in.
That’s a challenge: how do we visualise a curve in a 3D space that’s not like ordinary 3D space?
Aliens Need Lockdown Workouts Too
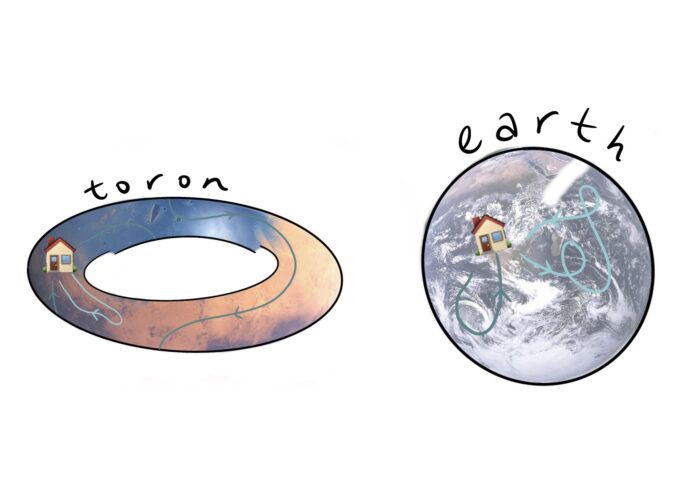
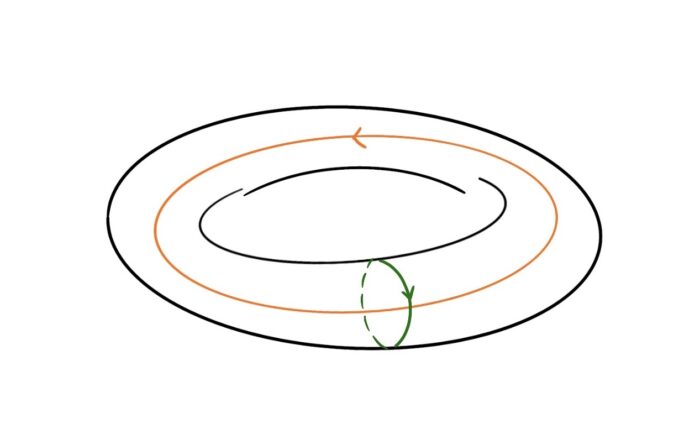
Kick it down a notch – how do we visualise a curve in a 2D space? ‘Ordinary’ 2D space (called R2) is like an infinite sheet of paper. A sphere is another example of a 2D space. Yet another example is a torus – the surface of a donut.
Let’s visualise how curves on a sphere are different to curves on a torus.
The inhabitants of Toron, a distant planet in the Kleig-IV Galaxy, are also coincidentally under stay-at-home orders due to the BOPID-94 pandemic. Each of them, like you, must plan their daily 60-minute walk.
How many loops can you walk from your home and return? How many loops can a Toronian walk?
Figure 3: Loops on a torus and on a sphere.
There are infinitely many paths you can take – it’d be a nightmare to describe all of them.
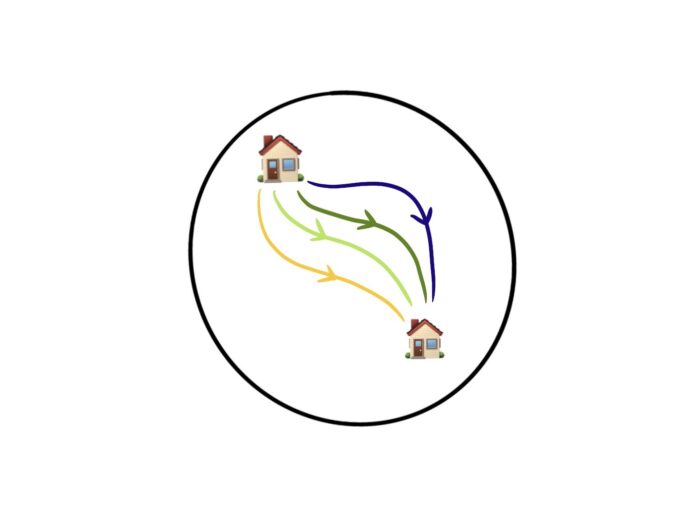
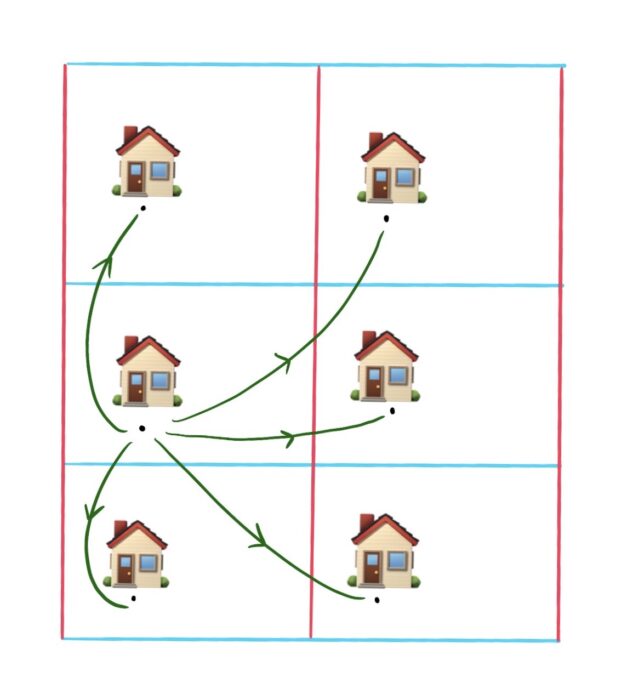
Instead, we’ll think about what makes two paths essentially the same, using the idea of homotopy. In this idea, two paths are equivalent if one can be deformed into the other. Look at the image below: imagine each path being a string connecting the two houses. If one string can be dragged to the position of another string, then those paths are considered homotopic, from the Greek homós meaning ‘same’ and tópos meaning ‘place’.
Figure 4: All of these paths on a sphere are homotopic to one another.
So, instead of asking “How many different loops can I walk?”, we ask “How many loops are there which aren’t homotopic to one another?”
On a sphere, any two loops are homotopic – you can always deform one loop into another. For example, you can always squish a loop into a single point. If someone gets on my case about not exercising, I say that sitting on my bed is homotopic to a 10km run.
The same is not true on a torus like Toron. Look at the loops below: they hug the donut in a way that they can’t be squished to single points. Sadly, a Toronian doesn’t have an excuse for not going on a 10km run.
Figure 5: Two loops on a torus that aren’t homotopic to single points
How many other different loops are there?
Unfolding a Torus
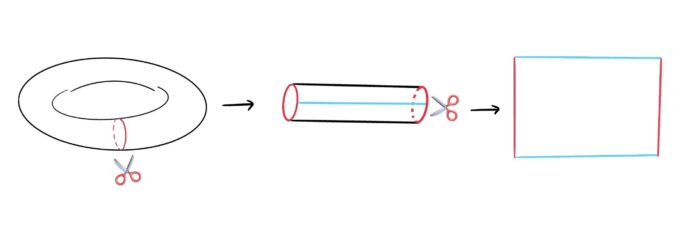
We will need a better way to visualise curves on a torus. We could mould a donut from clay and draw on that, but that’s too much effort!
Instead, think back to high school geometry – we can cut the torus into a net. Cut one circle out, and it becomes a cylinder. Cut open the cylinder, and it becomes a rectangular sheet of paper.
Figure 6: The net of a torus is a rectangle.
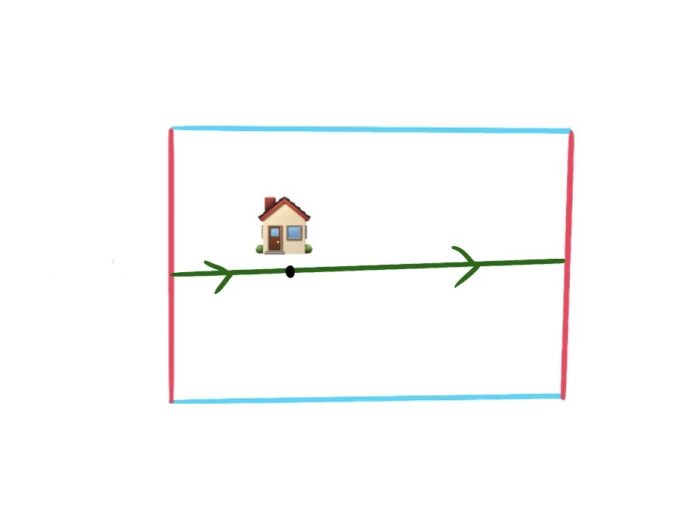
We can draw a Toronian’s exercise route as a curve on the net:
Figure 7: The red edges are glued together, as are the blue edges.
Note that, since the red edges were originally one edge (as were the blue edges), a curve that hits a red edge doesn’t stop, but jumps over to the other side of the rectangle. So, the green line in the picture is actually a loop!
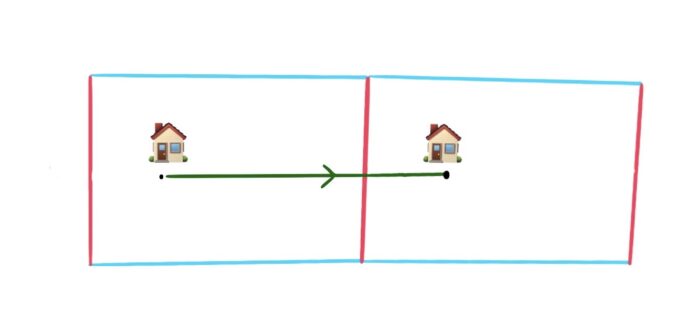
This can get hard to keep track of. There is a solution: stick another rectangle onto the edge and continue the curve into it.
Figure 8: The loop in the previous picture, drawn as a path between two copies of the same point.
This rectangle is supposed to represent the same rectangle, and each copy of our Toronian friend’s house is the same house. The curve drawn here starts and ends at a different copy of the house, but it’s really a loop starting and ending at the same house.
We can keep replicating the rectangle into an infinite grid, which is called the universal covering space for the torus. Any loop starting at the house can be drawn as a curve between two copies of the house in the infinite grid.
Figure 9: Each curve starts and ends at a copy of the original house.
Each of these curves represents a different loop that isn’t homotopic to the others. That means there are infinitely many loops a Toronian could choose to walk for their daily 60 minutes!
Let’s leave our alien friends alone for now – they’ve got a lot of exercising to do.
Four tricks in SO(3)
You might wonder what loops on a torus planet have to do with skateboard tricks.
The ideas of homotopy and covering spaces come from the field of algebraic topology, and they’re the same sort of techniques that the authors of ‘Topological Flips’ use to prove that there are only four flip tricks.
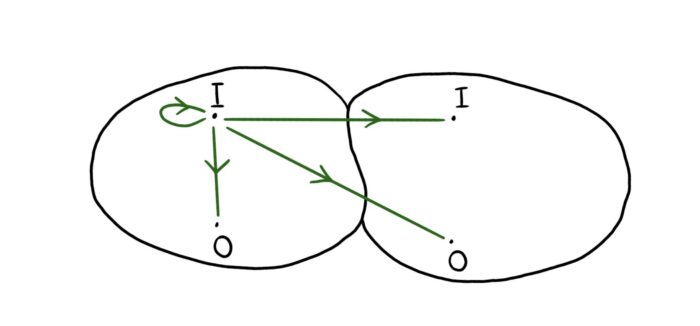
First, we cut SO(3) into a 3D net and replicate it. But it turns out that the net of SO(3) looks like half of a sphere, and you only need to put two – not infinitely many – together to make a full sphere.
To be clear, this is not what we usually call a sphere (which is a 2-dimensional surface), but a 3-dimensional sphere. We can’t draw this, but we can visualise it in a rough way:
Figure 10: Four paths representing four non-homotopic flip tricks.
Every flip trick is a curve starting at I and ending at I or O. On the universal covering space, there are two copies of I and two copies of O. Therefore, there are only four of these curves, and so only four skateboard tricks!
Specifically, the authors of ‘Topological Flips’ conclude that all skateboard tricks are homotopic to one of these four:
- Ollie
- Shove-it
- Kickflip
- Varial kickflip
What does this mean?
Of course, this proof doesn’t mean that skateboarders can only do four tricks, nor do the authors of ‘Topological Flips’ claim that it does. Their paper is about a mathematical model, and the answers you get out of a mathematical model are only as true to real life as the model is. In real life, homotopy is not a reasonable way to decide that two tricks are the same. A double kickflip is homotopic to an Ollie, but there’s no question that the double kickflip is a different and more impressive trick.
According to the authors, ‘Topological Flips’ is a proof-of-concept and they’re working on a more sophisticated mathematical model for skateboard flips. So, there’s still time for these mathematicians to drop a shocking revelation on the skateboarding world.
We acknowledge the Ngunnawal and Ngambri people, who are the Traditional Custodians of the land on which Woroni, Woroni Radio and Woroni TV are created, edited, published, printed and distributed. We pay our respects to Elders past and present. We acknowledge that the name Woroni was taken from the Wadi Wadi Nation without permission, and we are striving to do better for future reconciliation.